構造計算での「釣り合い」と「支点」について
釣り合うとは、どういう状態?
構造計算では〈釣り合い〉という言葉が、よく出てきます。
- 応力が釣り合ってる。
- 変形が釣り合ってる。
あなたが構造計算を経験していくと、どこかで目にするはずです。
それで、応力とか変形よりももっと基本的な〈構造物の釣り合い〉を今回はおぼえてしまいましょう。
ところで、「釣り合いがとれてる。」
この言葉を聞いて、あなたのアタマには何のイメージ画像が浮かびました?。

わたしは、シーソーが浮かびました。
シーソーが釣り合ってるとはどんな状態になっていますか?
誰がいますか?
何人いますか?
シーソーが釣り合ってるとは片方だけに人が乗ってませんね?
それで、両方に人が乗っていれば釣り合いますか?
・・・・・・
もう少しくわしい条件が必要ですね。
同じ人数でしょうか?
いえいえ、片方が大人一人で他方が小さい子ひとりならば釣り合いませんよね。
同じ重さの人が、同じ人数で両方に乗ったときに「釣り合ってる」となりますね。
構造物において「釣り合ってる」とは、すなわち「動いていないこと。」
どの方向にも動いていないことを3つの条件で言い表せます。
その3つとは?
・・・・・・・・
わかりました?
- 水平方向に動かない(=画面上でヨコに動かない)
- 鉛直方向に動かない(=画面上でタテに動かない)
- 回転しない(画面上で回転してない)
( )の表現はPCなどで見ている状態を想定して書きました。
この3つが成立している時に「構造物は釣り合ってる」となります。
構造物が釣り合う3つの条件を確実におぼえてしまいましょう。
支点の違いは何が違う?
上の3つを負担しているのが構造計算モデルでは「支点」と呼ばれる節点です。
支点には3つあります。
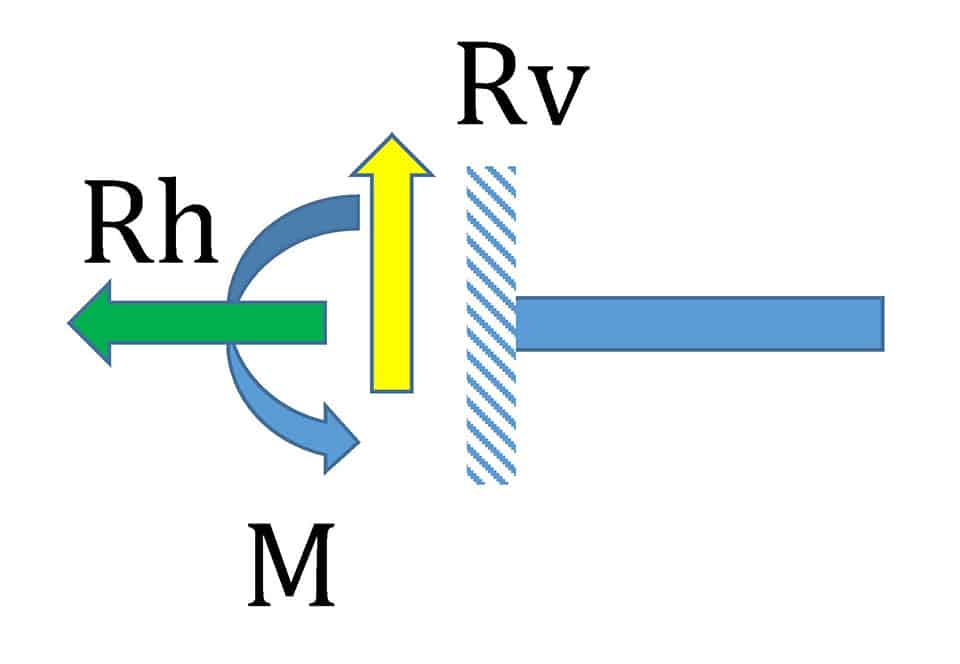
固定支点(水平/鉛直/回転を拘束)
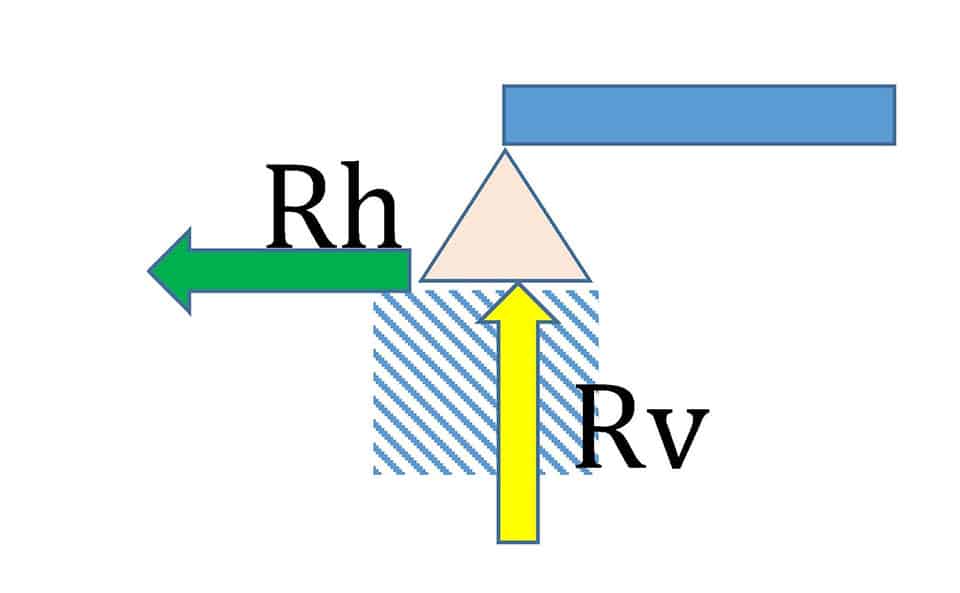
ピン支点(水平と鉛直だけ拘束)
ローラー支点(鉛直だけ拘束)
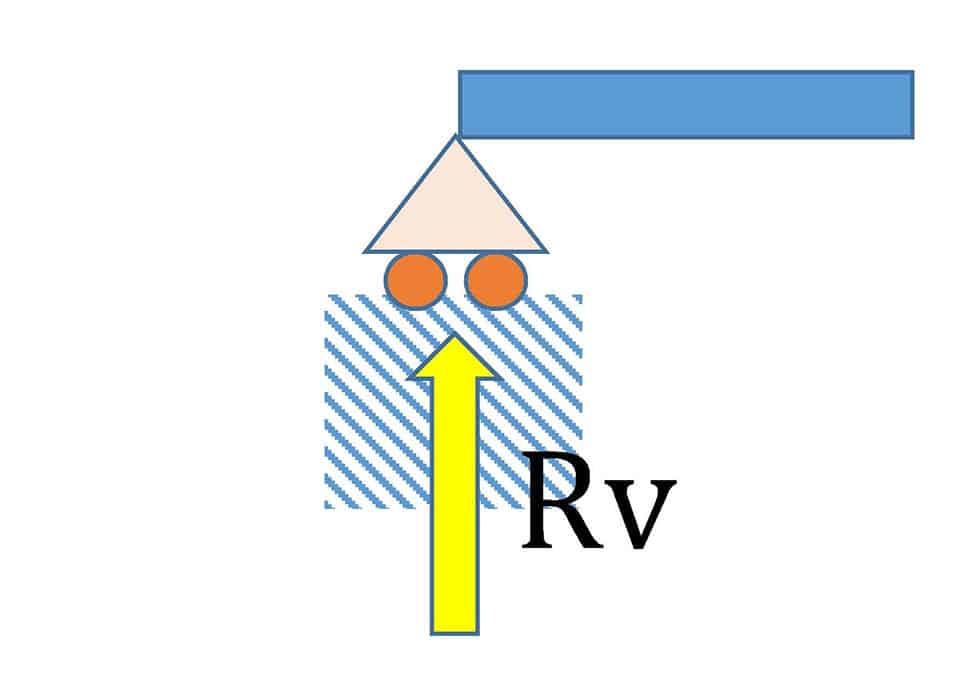
構造物の違いで支点の条件も変えなくてはなりません。
例えば、最も基本の「片持ち梁モデル」。
片持ち梁を支える支点はいくつありますか?
・・・・・・・・
そう、1つですね。
この1つの支点で前回の動かない3条件をクリアしないといけないわけです。
3つの支点の内で片持ち梁にマッチする支点は・・?
そう、固定支点しかありません。
では、単純梁モデルにいきます。
単純梁モデルは、支点が2つです。
2つあるので、回転が止まります。鉛直方向の動きも止まります。
水平方向は・・2つの支点をピン支点としますと、水平の動きも止まります。
ですが、水平方向の力が2箇所で止められるので、梁材に圧縮力が発生することになります。
梁材に圧縮力が生じますと座屈を考えなくてはなりません。
それで、1つだけローラー支点へ変えてみます。

こうしますと、梁材に軸力は発生せず
曲げモーメントだけ負担すればよいです。
片持ち梁から単純梁に変わると支点が2つに増えます。
支点が増えた分、支点一つが止めなければならない動きを少なく出来ます。
言い換えますと、支点一つの時には1点集中型で動きを止められるようにガッチリ作れば良い。
支点が増えた時にはお互いに負担を分け合うようにして支点を作れば良い。
という言い方もできますね。
支点の数の違いによる構造物の動きを止める役割の差。
このことをおぼえておきましょう。
『30代からは構造計算で年収UP』をキーワードに構造計算が『できない』を『できる!』へ、そして年収アップへと導く一級建築士・構造設計一級建築士です。こちらでもブログを書いています→ https://ameblo.jp/ryo3whisky




