構造計算で覚える２つの計算～「応力算出と断面算定」

応力算出の３ポイント

構造計算をマスターするには様々なアプローチがあります。

私は学術的な正確さよりも実務で使用に耐えうる実践的構造計算の手法を大事にしてます。

今回は、普段からお伝えしています実践的構造計算の基本で応力算出の３つのポイントをあらためて書きますね。

1) １モデル（２モデル）をマスター

まずは基本中の基本である「片持ち梁」。
このモデルは頭のなかでクリアにイメージ出来るくらいに焼き付けて下さい。

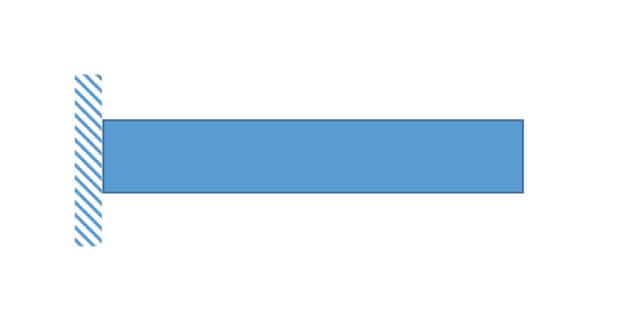
余裕があれば「単純梁」も頭の中へインストールしてください。

2) ２つの計算式をマスター

１つめは「曲げモーメント」の算出式（下記は片持ち梁集中荷重です）。

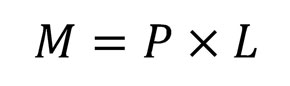
もう一つは「たわみ」の算出式（下記は片持ち梁集中荷重です）。

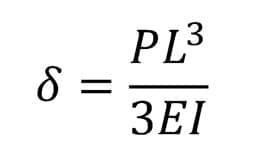
この２つの計算式を自分のモノとして下さい。

3) 荷重も２種類だけマスター

荷重は「Ｐ」か「ｗ」の２つ。
Ｐとは〈集中荷重〉point（点）のＰで覚えましょう。

ｗとは〈等分布荷重〉wide（幅：荷重が点ではなく広がってる）という意味でｗと覚えましょう。

以上の３つを書き出すことが出来るようになれば、実践的構造計算の初歩段階はクリア出来るようになります。

もう一度書きますね。

• １モデル
• ２つの計算式
• ２つの荷重

です。

---

断面算定での断面性能トリオ：Ｉ・Ｚ・ｉ

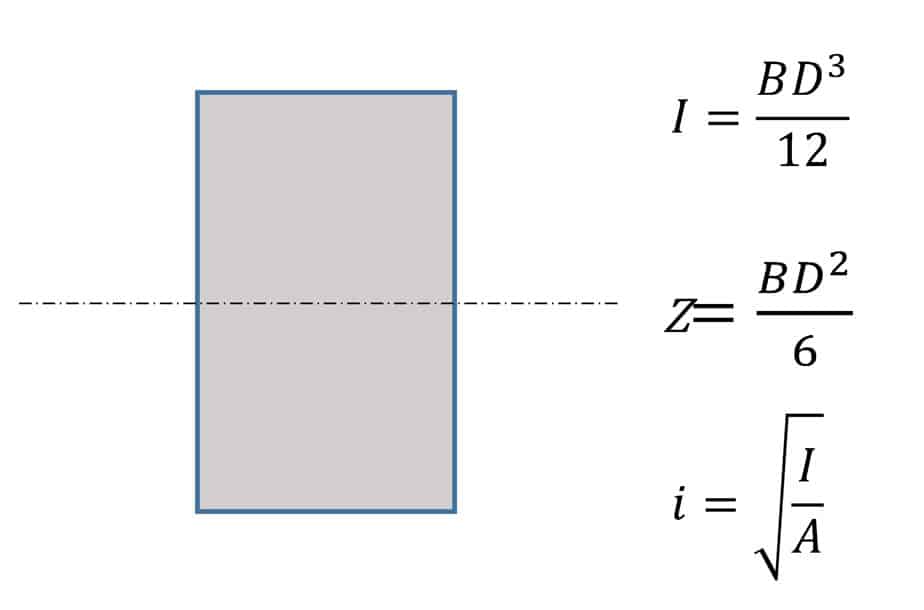
実践的構造計算では一つのモデルが大切だと何回もお伝えしていましたね。

そこで、今回は一つのモデルで出した応力から断面算定を行う時に、欠かすことの出来ない断面性能３兄弟をお伝えします。

その３兄弟とは

• 断面二次モーメント：Ｉ
• 断面係数：Ｚ
• 断面二次半径：ｉ

です。

まずは、長男　「断面二次モーメント：Ｉ」（下記は長方形断面）

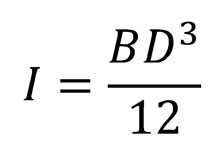
この断面性能が必要になるのは部材の変形量を算出するときです。
部材の変形量＝たわみですね。

もっと平たく言えば「部材の曲がり難さ」を決める値です。

断面二次モーメントの値が大きいと部材は曲がりにくくなります。
値が小さいと部材は曲がりやすくなります。

つぎに次男坊　「断面係数：Ｚ」（下記は長方形断面）

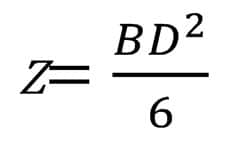
こちらは、計算した応力から部材の応力度を導くのに使う断面性能です。

ひとことで言うと「部材の強さ」を決める値です。

断面係数の値が大きければ、同じ応力では応力度が小さくなります（より強い）。断面係数値が小さいと応力度が大きくなります。

それから末っ子の　「断面二次半径：ｉ」（下記は長方形断面）

断面二次半径は、圧縮とねじりの力に関係します。
圧縮の力では、「座屈」という現象の境界を決める値です。

同じ部材長さで断面二次半径値が小さいと座屈しやすいです。
断面二次半径値が大きいと座屈しづらいです。

以上断面性能３兄弟を書きました。
その中でも

• 断面二次モーメント：Ｉ
• 断面係数：Ｚ

の長兄と次兄は、実践的構造計算で決して欠かすことの出来ない断面性能です。

しっかり自分のモノにしておきましょうね。