構造計算で使う2つの荷重について。

構造計算を行う時に荷重は必須です。
荷重を表す構造力学上での種類はいくつかあります。
集中荷重/等分布荷重/等変分布荷重/移動荷重/面荷重
しかし、実践的構造計算ではすべてを使って解く必要もなく、
割り切って考えれば集中荷重と等分布荷重の2つで事足ります。
その2つの荷重のうちで集中荷重について。
◆なぜ集中荷重は矢印なのか?
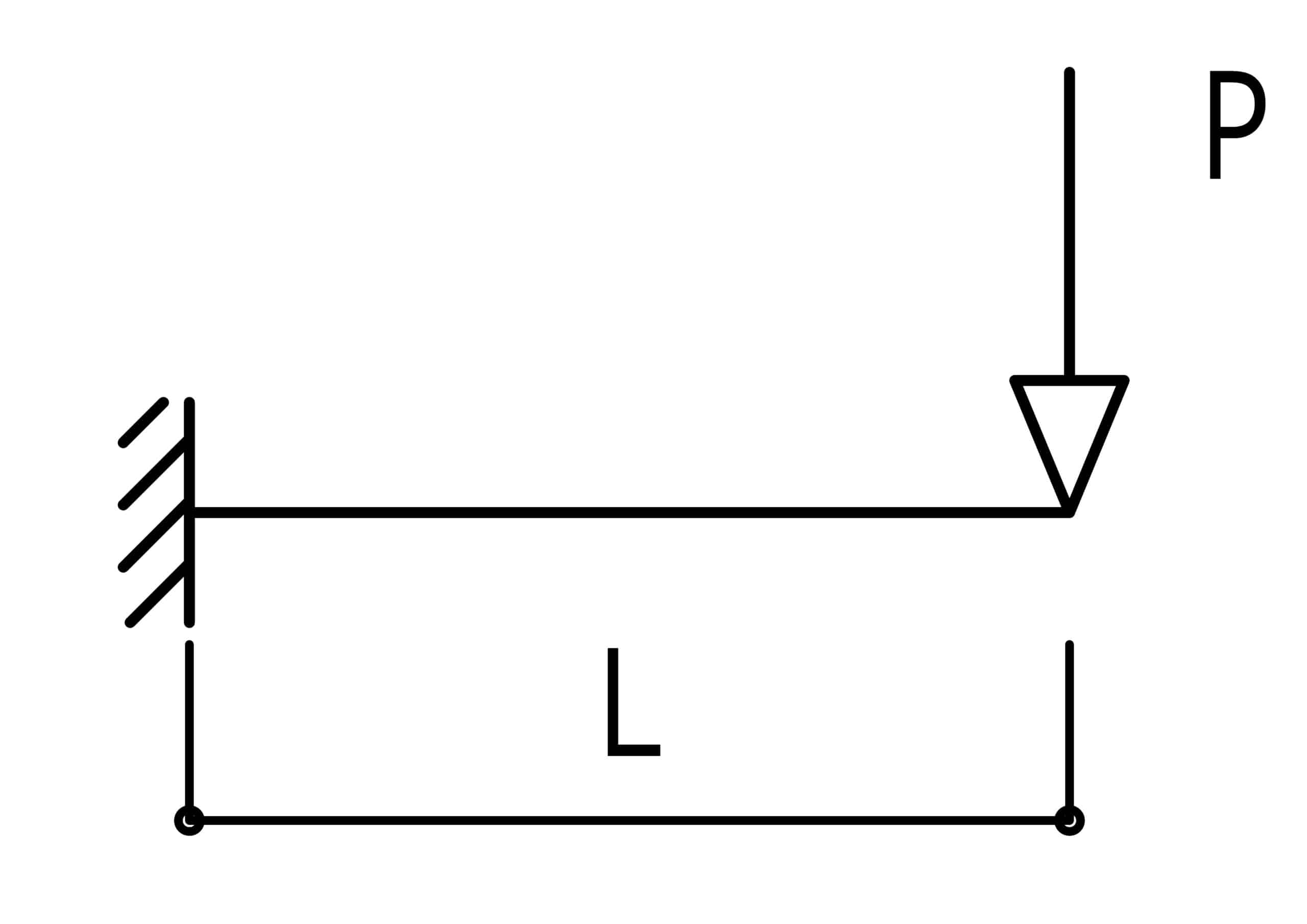
集中荷重は矢印で表記します。なぜ、矢印で表すのでしょうか?。
ここで、とても大切なことは
荷重と呼ばれるには3つの条件を満たしている必要があります。
それは、
・大きさ
・方向
・作用する位置 です。
そして荷重には必ず〈単位〉が付きます。
集中荷重の単位は[N(ニュートン)]
あるいは[kN(キロニュートン)]です。
構造計算は現実に存在しようとする構造物(建物/工作物)を扱いますね。
現実に存在するとは幅/長さ/厚み が測れます。
そして「ある物質」で作られてます。
物質には比重(密度)という
水1立方メートルに対しての重さが定義づけされてます。
なので、構造計算を行う部材に載る重さは
「幅×長さ×厚み×比重」で表せます。
幅/長さ/厚みは単位が[m]や[mm]
比重は[kN/m3]や[N/mm3] で上の掛け算通りに行えば「kN]、[N]になります。
幅と長さと厚みを〈集約して〉1つの箇所にピンポイントで作用させる。
そして荷重としての3つのルールで表現するから〈矢印〉になるんですね。
ほら、カンタンでしょう?。
◆なぜ等分布荷重は線で書くのか?
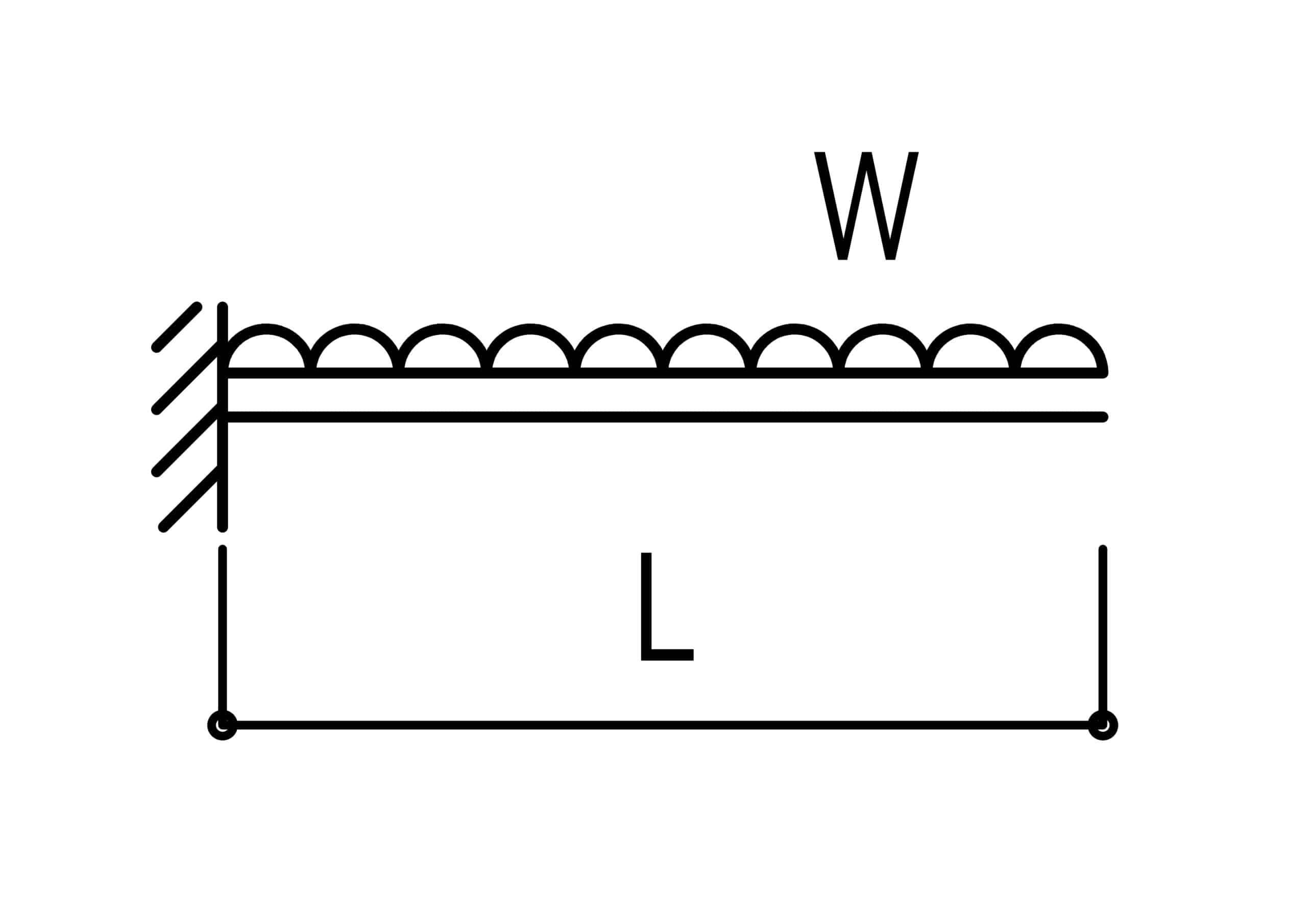
上段では集中荷重を矢印で表記する理由についてお伝えしました。
ここでは、構造計算での荷重表現の双璧を成す、もう一つの荷重。
等分布荷重について書きます。
等分布荷重という荷重の意味は、すでにご理解されてますか?。
今一度おさらいを兼ねて書きます。
等分布荷重とは
〈構造計算対象の部材に対して
部材の長さ全体に一定の量で掛かる荷重〉です。
部材のどこを切り取っても掛かっている荷重が存在してます。
前回の集中荷重は、ある一点に作用でしたね。
なので、部材の中には荷重がかかっていない箇所が存在してます。
それで、この等分布荷重。
実践的構造計算での表現は波線/一本線で表します。
より精密に表現しますと、矢印を部材の長さ全体に行き渡るよう並べたりします。
単位は[kN/m]や[N/mm] です。
実務では[kN/m]が多いですね。
たとえば、風荷重。
基準風速をもとに風圧力を出しますと
w=1000[N/m2]などと算出できます。
これは1平方メートルあたり1000Nの風が当たってくることを指します。
いわゆる面荷重ですね。
一方で受ける側の梁あるいは間柱は部材の長さ全体で抵抗します。
そこで計算をカンタンにするために
面荷重を部材全般に対しての荷重へ幾つになるのかを求めるわけです。
求め方は〈面荷重に幅をかける〉たったこれだけのこと。
面荷重:[N/m2] × 幅:[m]で、等分布荷重:[kN/m] です。
一つの方向に連続しているから〈線〉状になるわけですね。
そして応力計算でモデル図を書くときに
カンタンに表現するために「一本線」で書いているのです。
カンタンな理屈でしょう?。
『30代からは構造計算で年収UP』をキーワードに構造計算が『できない』を『できる!』へ、そして年収アップへと導く一級建築士・構造設計一級建築士です。こちらでもブログを書いています→ https://ameblo.jp/ryo3whisky


