RCスラブの構造計算：正方形と長方形のどちらが有利？

鉄筋コンクリート（ＲＣ）のスラブについて

スラブの平面形状は四角形であることがほとんどです。
四角形には正方形と長方形が含まれてますね。

では、スラブの平面形状が正方形と長方形でどちらが有利になるのでしょうか？

結論から言いますと、ＲＣスラブの構造計算では
「短辺と長辺の長さが等しい正方形スラブは要注意」
という特徴があります。

なぜでしょうか？今回はその根拠について考察していきましょう。

（１）必要最小となる厚さから

ＲＣスラブは鉄筋コンクリート構造計算規準で必要最小となる厚さを求める式があります。

2010版のRC規準で18条の（解18.4）式です。

この計算式に短辺の長さと長辺の長さから
辺長比：λ（ラムダ）=Ly（長辺） / Lx（短編）
を求めて、スラブ自重外の重さと短辺の長さを代入していくと算出できます。

一見、複雑にみえる式ですけれど計算にトライしてみて下さい。

辺長比が2のとき、1.5のとき、1のときの３つを比較してみますと「辺長比：1」のケースで、必要となる厚さが増えていく度合いが大きいです。

この様子を説明している図が鉄筋コンクリート構造計算規準2010 P.261「解説図18.1」になります。

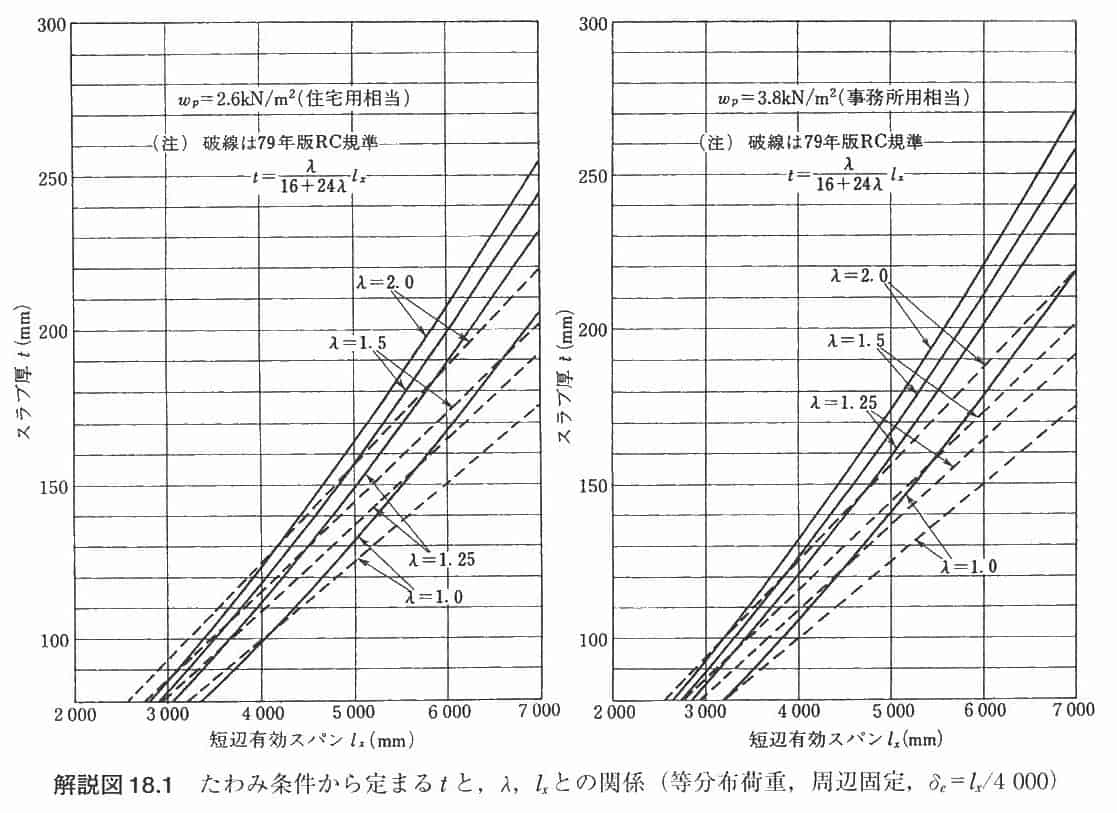
実は、たわみ条件からスラブ厚さが決まってる一面があるのですね。この図表からは、短辺の長さが短い時には辺長比の違いで必要スラブ厚さに差はあまり見られません。

しかし、スパンが5.0mあたりからは辺長比1.0と2.0とでは差が開いてきてます。

（２）必要となる配筋から

スラブの配筋は、生ずる曲げモーメントで決まります。
曲げモーメントの計算は計算式で行う「算式解法」と図表を使って求める「図式解法」があります。
今回は図表を使ってみます。

「等分布荷重時四辺固定スラブの応力図」
という図表（たいがいの市販の構造計算の本に載ってます）より各辺のスラブの応力が出せます。

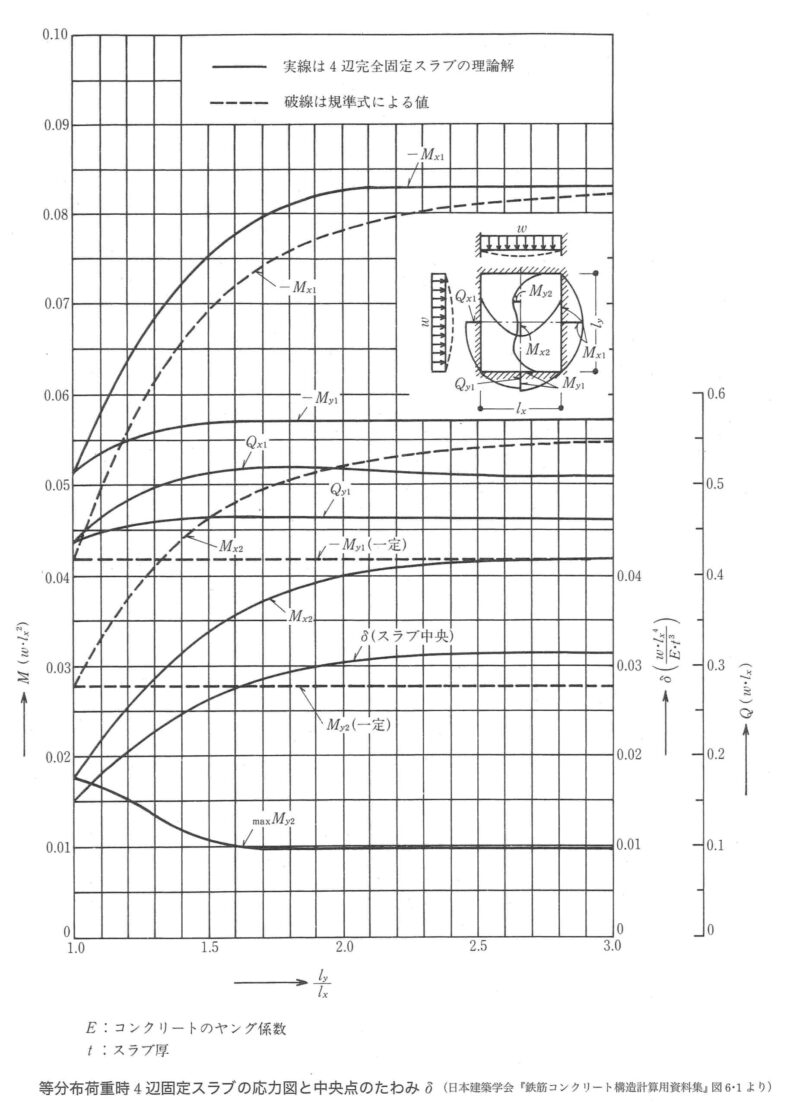
この表でも着目してほしいのは辺長比です。

辺長比：λ（ラムダ）=Ly（長辺） / Lx（短編）

Ly/Lxの比率で1.0、1.5、2.0のラインを見て下さい。
MxとMyの値が2.0へ移るほど開いていることが確認できますよね。

ということは、
辺長比が1.0では短辺と長辺の応力が等しい。
よって、配筋も同じ径で同じピッチともいえます。

辺長比2.0では、応力値の差が大きいので
短辺と長辺の配筋は同一径と同一ピッチでは一方に余裕ありすぎとなります。

実際に計算するとわかるのですけど、短辺の配筋が鉄筋量として多く必要です。

（１）と併せて考えますと、
短辺の長さが長くなる辺長比：λ＝1.0のスラブの配筋が最も鉄筋量を必要としてきます。

いかがでしょうか？

まとめますと
「必要最小となる厚さ」「必要となる配筋」の両方の観点から、
「短辺と長辺の長さが等しい正方形スラブは要注意」
という特徴が確認できましたね。

今回は、実際の構造計算での内容についてお伝えしました。