ヤング係数とは

ヤング係数って何？

今回は「ヤング係数」のお話です。

ヤング係数は応力と変形に関わってくる値で、構造計算を行う上で欠かすことのできない値です。

まずは、実践的構造計算の初歩段階でマスターしたい計算モデルである「片持梁構造」を例に、「ヤング係数とは何か？」からご説明しましょう。

片持梁先端に集中荷重：$P$ を受けた応力計算の式で曲げモーメントを出すには

$M=P \times L$

で表せましたね。

とても簡単（シンプル）な式です。

同じモデルで梁の変形を求めるには

$δ=PL^3/3EI$

でしたね。

$P$は荷重、$L$は部材の長さ（＝スパン）、$I$は断面二次モーメント。

そして、残った「$E$」という記号がヤング係数です。

このヤング係数、別名を

• 縦弾性係数
• ヤング率
• Ｅモジュール

などと呼んでいたりもします。

ヤング係数のヤングとは「若い」・・という意味ではありません。人の名前から来ています。

トーマス・ヤングという人物でもともとは物理学を専門とした人。才能がものすごくあったらしく、物理学以外に医学、生物学、果てには諸外国語まで使いこなした人のようです。

ヤング係数は、何を意味する？

では次に、ヤング係数って何を意味するのか？を考えてみましょう。

皆さんは「フックの法則」を覚えていますか？フックの法則とは「力と変形が比例関係になる」という法則でしたね。すなわち、ある物体に力が加われば変形が生じるという関係です。

数式で表しますと、力：$F$ 、変形：$x$
比例関係になるので何らかの係数：$K$ とすると

$F=K \times x$ で示せます。

$K$の値をバネ定数と呼んだりします。

ここからのお話は、物体に外力が作用→応力が発生→変形が生じる というフローの中で、応力と変形にフォーカスしますね。

変形とは物体の形が変わることで、別の言い方をしますと「ひずむ（漢字で歪む）」と言い表せます。ひずむは動詞ですので名詞に変えますと「ひずみ（歪み）」です。

この応力とひずみがフックの法則と照らし合わせるように表現すると、ヤング係数を求める式になります。

力：$F$ を 応力度：$σ$ へ置き換えます。

変形：$x$ を ひずみ：$ε$（イプシロン）へ同じように置き換えます。

フックの法則の公式は
$F=K \times x$ でしたので、上のσとεを入れ換えてみます。
$σ=? \times ε$ となります。

上の置き換えた式の「？」に入るのがヤング係数：$E$ になります。

すなわち、
$σ=E \times ε$　で表されます。式変形すれば
$E=σ/ε$ となります。

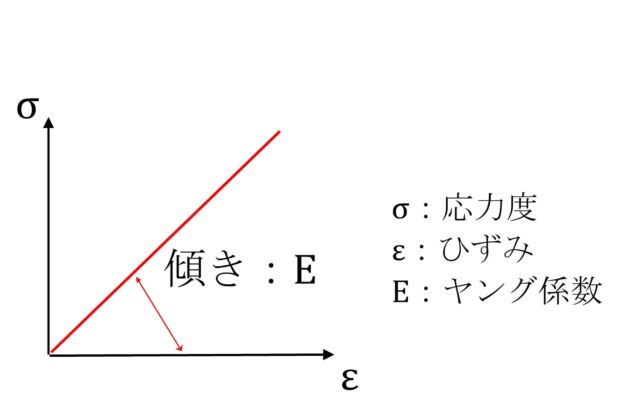
つまり、ヤング係数とは『バネ定数と似たような値』なのだということが、上の式から読み取れますよね。

ただし、フックの法則のバネ定数もヤング係数も「材料が白旗を上げる」前までのところで成立することが条件です。材料が白旗を上げるとは「降伏する」ことを指します。

材料が伸びても元に戻る現象の範囲内で成り立つ公式だということを覚えておいてくださね。

材料ごとにヤング係数は求めるの？

構造計算で扱う建築材料は、鋼／コンクリート／木 などが主ですね。この建築材料ごとにヤング係数は存在します。

では、材料ごとにヤング係数を求めるには前回までの式を使って求めていくのでしょうか？

答えは、計算して求めません。もう既に材料ごとに試験（引張試験）を行って、ヤング係数を算出してあります。

では、材料ごとのヤング係数は何を調べればわかるのか？

ひとつは計算規準に掲載されてます。鋼構造計算規準とか鉄筋コンクリート構造計算規準を開いていくと材料の項目に載ってます。

すこし範囲を広げて建築材料以外のヤング係数を知りたいならウィキペディアにも載ってます。「ヤング係数」で検索してみて下さい。
ウィキペディアのヤング係数は単位が $[Gpa]$ となってます。「ギガ パスカル」ですね。

脱線ついでに単位を変換してみましょう。

まずは$G$（ギガ）について。

携帯電話のＣＭなどで「ギガ割引」とか耳にしたことがありますよね。あの、ギガと同じです。ギガは１０の９乗（１の後に０が９個）の数です。

$[Gpa]$ を構造計算でつかう $[N/mm2]$ へ変換しますと

$1 [pa] =1 [N/m^2]$
$=1.0 \times 10^{-6}[N/mm^2]$　　です。

一方で、
$1[Gpa] = 1.0 \times 10^9[pa]$　なので、

上の二つを合体させると

$1[Gpa]=1.0 \times 10^{(9-6)}$
$=1.0 \times 10^3[N/mm^2]$　　です。

ウィキペディアの鋼は201～216［Ｇｐａ］と幅があります。鋼構造計算規準では
$2.05 \times 10^５[N/mm^2]$ です。

ウィキペディアにならって表しますと
$2.05 \times 10^５[N/mm^2]$
$=2.05 \times 10^{(5-3)}$
$=2.05 \times 100$
$=205[Gpa]$　となります。

パスカルは構造計算では少し馴染みが薄い単位になりますね。単位変換だけは確実に行いましょう。

ここまで、鋼について書きました。今度はコンクリートです。

コンクリートのヤング係数（ $Ec$ ）は、比重とコンクリート強度による計算式にて算出します。

下の式になります。

$Ec=3.35 \times 10^4 \times (γ/24)^2 \times (Fc/60)^{1/3}$

比重：$γ$ は決まってます。→（ $γ=23$ ）
コンクリート強度も使う強さが区分されてます。

設計基準強度：Fc21N ならば
計算式にてもとめると
$E=21682[N/mm^2]$　　になります。

ヤング係数には縦があるなら横もあるの？

ところで、ヤング係数には「縦弾性係数」という呼び方もありましたよね。この縦弾性係数という漢字から、ヤング係数というのは
部材の垂直（材軸）方向にかかる力に対して部材応力が発生し、
縦ひずみが生じた現象に対して成立する法則
ということがわかってます。

それならば、『縦があるなら横もあるの？』と、カンのいいあなたなら質問がアタマに浮かんだのでは？

いい質問ですね～。

じつは・・・あります。

「横弾性係数」という呼び方が一般的かは明確ではありません。

物体に作用する力で垂直方向（材軸方向）は「圧縮／引張」と呼ばれる力です。では、水平方向に作用する力は何と呼ばれるでしょうか？

それは、「せん断力」ですね。紙をハサミで切る時の力です。

ここで、サイコロのような物体をイメージしてみましょう。このせん断力が物体に作用した時にどのような変形をするかといいますと
“ミニョ(？)”って感じで「ひし形（平行四辺形）」のように変形します（豆腐を横から押すイメージ）。

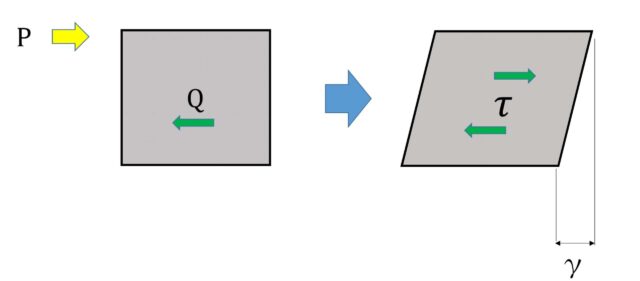
この時の変形量を $γ$（ガンマ）で表し
物体に生じたせん断応力度を $τ$（タウ）で表現します。
（ガンマもタウもギリシャ文字です。「なぜ、ギリシャ文字も使うの？」という疑問はまた次の機会で。）

ヤング係数：$Ｅ$ はひずみ：$ε$ と垂直応力度：$σ$ で表すと
$E=σ/ε$　でしたね。

同じように物体がせん断力を受け、変形した時にはフックの法則に照らし合わせて
横弾性係数＝せん断応力度／せん断変形量
の関係が成立します。

この横弾性係数を別名で『せん断弾性係数：$G$』と呼びます。

上の横弾性係数をアルファベットとギリシャ文字で表しますと

$G＝τ/γ$　　となります。

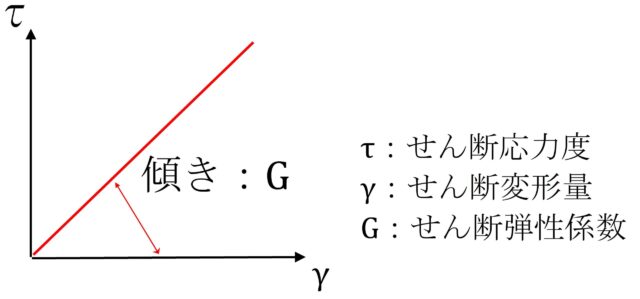
ヤング係数ほど頻ぱんに出てくる係数ではありませんけれど、部材のねじりだとか土の変形を扱うような時には出てくる数値です。いまは、一つの知識としてとらえておいてくださいね。

今回は、構造計算で欠かせない「ヤング係数」について、基本からかなり深掘りしたところまで詳しくお伝えしました。長いブログになりましたが、

という点だけ、覚えておきましょう。