構造計算での間違いを減らしてカンタンに行うには？

◆構造計算の単位。そろえてないのが間違いの元

以前に構造計算のセミナーを行った経験から、、、。

セミナーでの計算演習でも見受けられたのは計算作業でのカンタンなまちがい。

構造計算に慣れていない方は出てくる数のケタの多さに緊張し、

ケタ数が１ケタ変わるだけで計算される結果がビックリするものになります。

たとえば、たわみの計算。
ヤング係数を１ケタ小さくしたのならば
結果として出る変位は、本来の１０倍です。

梁の中央たわみが１ｃｍ（１０ミリ）のところを
「１０ｃｍもたわんでしまう！」となります。

計算でのカンタンな間違いを
「ワタシのアタマが良くないから。」
とか
「オッチョコチョイな性格だから間違うんだ。」
などと

あなた自身へフォーカスして自分を責めるのは少し待ちましょう。

計算でのカンタンな間違いの元。
それは、

あなたの能力や性格の問題ではなく
原因は「単位を揃えていない。」ことにあったかもしれません。

先ほどのたわみの計算で、

荷重の単位は[ｋＮ]で与えて、ヤング係数は[N/ｍｍ^２]、
さらに断面二次モーメントは[ｃｍ^４]

などとして計算していては間違うのも当たり前です。
（私でも間違えます。）

それをスッキリと単位をそろえて
みるといかがでしょうか？。

荷重は［Ｎ］、ヤング係数は[N/ｍｍ^２]、断面二次モーメントは[ｍｍ^４]

［Ｎ］と［ｍｍ］だけになりましたので
計算結果が１０倍違うという間違いは避けられるようになりますよ。

◆計算をカンタンにするのは指数

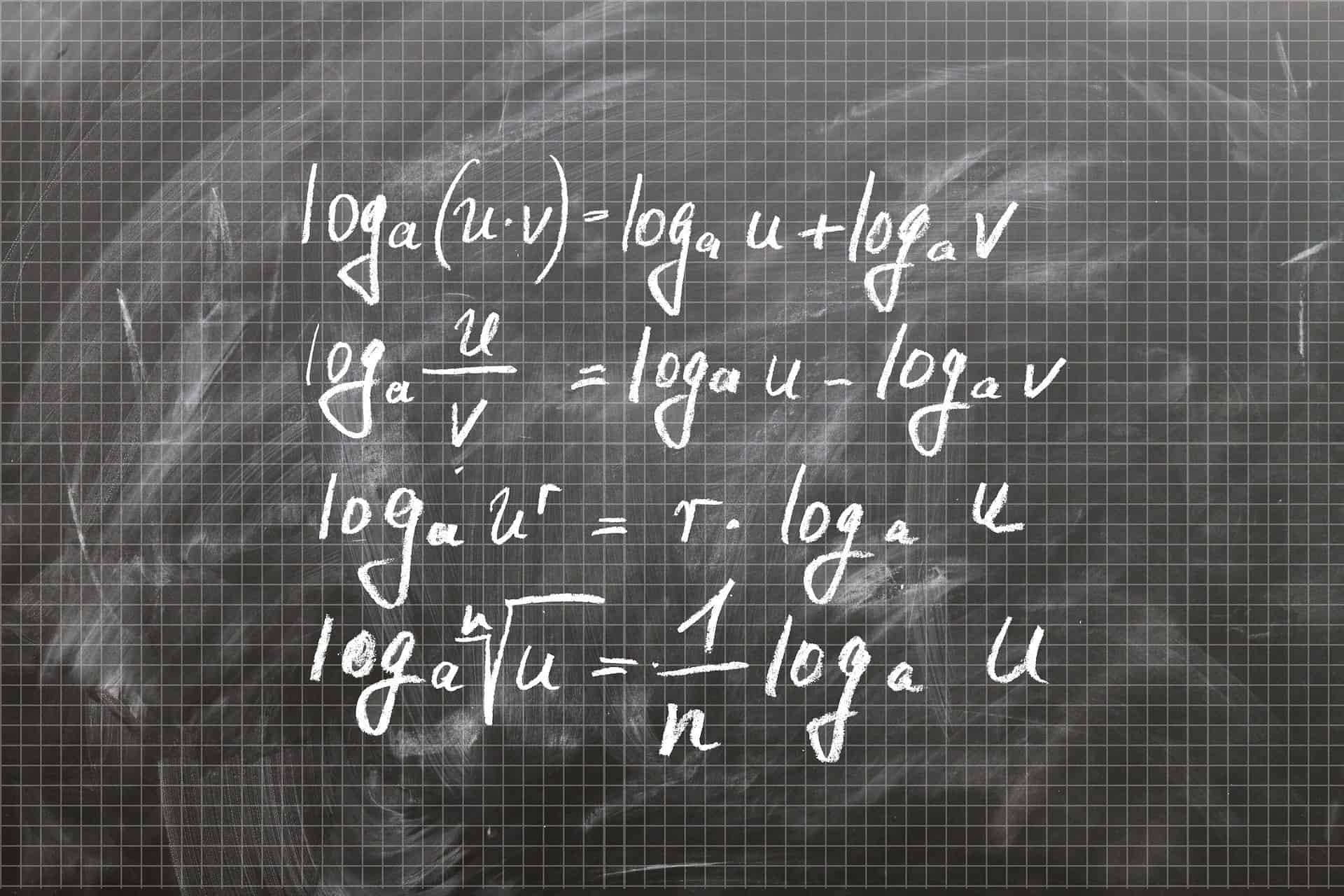
ＳＩ単位での構造計算では数値のケタが多くなりますね。

とくに、Ｎ（ニュートン）とｍｍ（ミリ）を使っていますと、、、。
ケタの多さに「あぁ～！！」って言いたくもなります。

「電卓で計算するから大丈夫。」
という声を以前に聞いたことあります。

しかし、電卓で計算するからとはいえ
押し間違いが無いとは言えません。

そこで、ＳＩ単位での構造計算を
カンタンにする方法として
〈指数〉を使ってみてはいかがでしょうか？。

「指数？」って、あなたのアタマに疑問符が浮かびましたか？。

そう、指数です。
「ａのｎ乗」って呼ぶやつです。

例えばヤング係数。
鉄骨のヤング係数は２０５，０００［N/mm^２］
これを２．０５×１０⁵（１０の５乗）　と表しておくのです。

断面二次モーメントも同じです。
鉄骨Ｈ形鋼：H-400ｘ200ｘ8ｘ13は
Ｉｘ＝２３５，０００，０００［mm^４］
これを２．３５×１０^８（１０の８乗）　と表しておくのです。

指数の良いところは
・指数同士の掛け算は足し算に。
・指数同士の割り算は引き算に。
というルールが有ること。

なので、上のヤング係数と
断面二次モーメントの掛け算は

指数ならば、
２．０５×２．３５×１０^{（５＋８）}
と書けるわけですね。

そうなると電卓使うよりも
「だいたい４の１３乗か」と予測が付きます。

それとの一つのポイントは
「元の数の上２ケタの数字をとって
　あとは１０の何乗」とすること。

もちろん、上の１ケタなら整数なので
九九で求められます。
（ただし、精度は少しだけ緩くなります。）

でも、一般的な構造計算では
厳密解を出すということは求められません。

それよりもケタ間違いや押し間違いによる
繰り返し計算をなくす方が効果的だと思いますよ。